Number sequences are sets of numbers that follow a pattern or a rule.
Each number in a sequence is called a term.
A sequence which increases or decreases by the same amount each time is called a linear sequence. Non-linear sequences do not increase by a constant amount. They include quadratic sequences.
Before reading this guide, it may be useful to read the guide from Module 6 (M6) on sequences.
Non-linear sequences
Some sequences may contain terms that are fractions.
Example
Work out the \(nth\) term of the following sequence: \(\frac{1}{3}, \frac{2}{5}, \frac{3}{7}, \frac{4}{9} …\)
First, look for the pattern on the numerator of each fraction.
| Position | 1 | 2 | 3 | 4 |
| Term | 1 | 2 | 3 | 4 |
The rule is \(n\).
Then, look for the pattern on the denominator of each fraction:
| Position | 1 | 2 | 3 | 4 |
| Term | 3 | 5 | 7 | 9 |
The rule is \(2n + 1\).
The rule for the sequence \(\frac{1}{3}, \frac{2}{5}, \frac{3}{7}, \frac{4}{9} …\) is \(\frac{n}{2n + 1}\).
Generating a quadratic sequence
The \(nth\) term for a quadratic sequence has a term that contains \(n^{2}\). Terms of a quadratic sequence can be worked out in the same way.
Example
Write the first five terms of the sequence \(n^{2} + 3n – 5\).
when \(n = 1, n^{2} + 3n – 5 = 1^{2} + 3 \times 1 – 5 = 1 + 3 – 5 = –1\)
when \(n = 2, n^{2} + 3n – 5 = 2^{2} + 3 \times 2 – 5 = 4 + 6 – 5 = 5\)
when \(n = 3, n^{2} + 3n – 5 = 3^{2} + 3 \times 3 – 5 = 9 + 9 – 5 = 13\)
when \(n = 4, n^{2} + 3n – 5 = 4^{2} + 3 \times 4 – 5 = 16 + 12 – 5 = 23\)
when \(n = 5, n^{2} + 3n – 5 = 5^{2} + 3 \times 5 – 5 = 25 + 15 – 5 = 35\)
The first five terms of the sequence: \(n^{2} + 3n – 5\) are \(–1, 5, 13, 23, 35\).
Finding the nth term of a quadratic sequence
Find the \(n^{th}\) term of the sequence \(3, 6, 11, 18, 27, …\)
1. Work out the first difference.
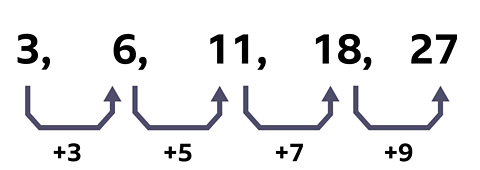
For this sequence the first difference is not common that means it is not linear.
2. Work out the second difference.
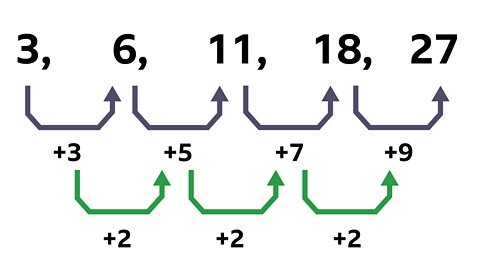
The second difference is common, which means that the sequence is quadratic.
3. Find the coefficient of the \(n^{2}\) term by dividing the second difference by 2.
In this sequence, the coefficient of the \(n^{2}\) term will be 1.
The \(n^{th}\) term begins with \(1n^{2}\) or just \(n^{2}\)
4. Think about the sequence \(n^{2}\) – \(1, 4, 9, 16, 25\)
How does this compare with the sequence \(3, 6, 11, 18, 27\)?
This sequence is 2 more than \(n^{2}\).
So the \(n^{th}\) term of the sequence \(3, 6, 11, 18, 27, …\) is \(n^{2} + 2\)
Example
Find the \(n^{th}\) term of the sequence \(–1, 4, 11, 20, 31, …\)
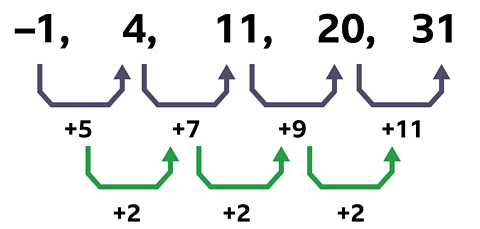
First difference is not common, so the sequence is non-linear.
Second difference is 2, so the \(n^{th}\) term begins with \(n^{2}\)

Think about the sequence \(n^{2}\).
How does this compare with the sequence \(1, 4, 11, 20, 31, …?\)
Different numbers are added each time. Think about these numbers as a sequence and find the \(n^{th}\) term of the sequence.

The sequence begins with \(n^{2}\) and then adds a linear sequence \(2n – 4\)
The \(n^{th}\) term of the sequence \(–1, 4, 11, 20, 31, …\) is \(n^{2} + 2n – 4\).
Test yourself
More on M7: Number
Find out more by working through a topic