Before reading this guide, you may find it useful to revisit the guide from M1 on equations, the guide from M2 on equations, and the guide from M6 on simultaneous equations.
Simultaneous equations
Simultaneous equations are two or more equations with two or more variables.
They are simultaneous because they can be solved to give values for the variables that are equal in each equation.
This is clearly demonstrated in Module 6 (M6) by solving simultaneous equations graphically.
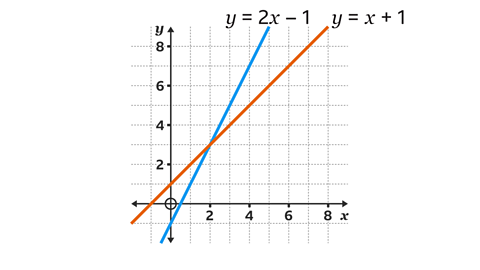
The solution to the equations
\(y = 2x – 1\) and \(y = x – 1\)
is when \(x = 2\) and \(y = 3\)
\((2, 3)\)
At Module 7 (M7), simultaneous equations may be solved algebraically.

Solving simultaneous equations algebraically by elimination
The most common method for solving simultaneous equations is the elimination method which means one of the unknowns will be removed from both equations. The remaining unknown can then be calculated.
- Eliminate one of the letters from both equations by adding or subtracting
- Calculate the value of the remaining letter by solving the equation
- Substitute this value back into one of the equations to find the value of the other letter
Example
Solve the following simultaneous equations.
\(3x + y = 11\)
\(x + y = 5\)
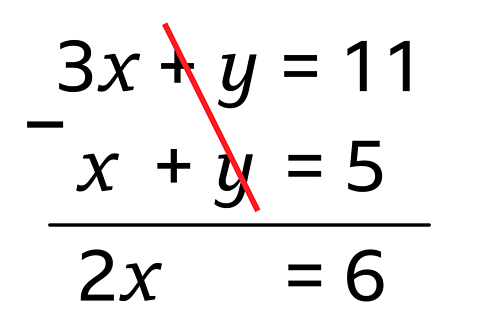
Solution
Eliminate one of the letters from both equations by adding or subtracting. This can be done if the coefficientThe number giving the quantity of a given variable or combination of variables. For example, 5 is the coefficient of 5*n*. of one of the letters is the same, regardless of sign.
In this example both equations have \(+y\)
A way to remember this is same signs subtract, different signs add.
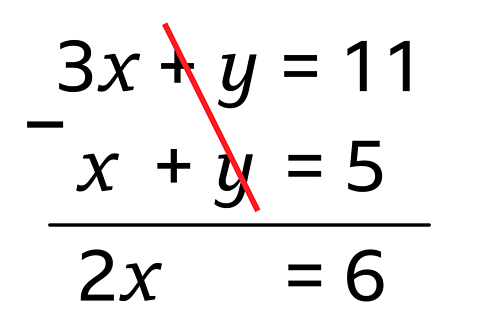
- Calculate the value of the remaining letter. Since they are both positive the equations should be subtracted to eliminate \(y\).
\(2x = 6\)
\(x = 3\)
- Subsitute this back into one of the equations to find the value of the other letter.
\(x + y = 5\)
When \(x = 3\)
\(3 + y = 5\)
\(y = 2\)
Answer
\( x = 3 \)
\( y = 2 \)
This can be checked by substituting the values into the other equation.
\(3x + y = 11\)
\(3(3) + 2 = 11\) – this is correct
Example
Solve the simultaneous equations.
\(5a + 4b = 10\)
\(6a – b = –17\)
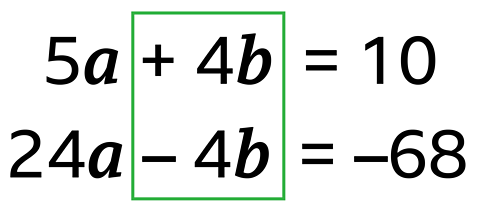
Solution
Before eliminating, one of the letters must have the same coefficient in both equations.
The second equation will need to be multiplied by 4 in order to have the same number of \(b\)s. Sometimes it is necessary to multiply both equations.
\(6a – b = –17 (\times 4) \rightarrow 24a – 4b = –68\)
- Eliminate one of the letters from both equations by adding or subtracting
Same sign subtract, different signs add
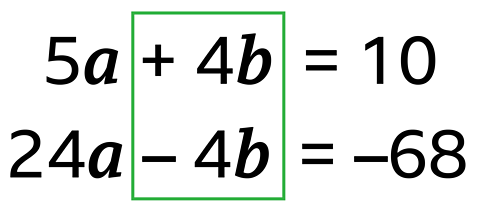
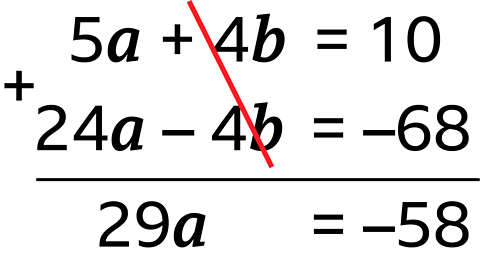
The signs on the \(4b\) are different, so add to eliminate.
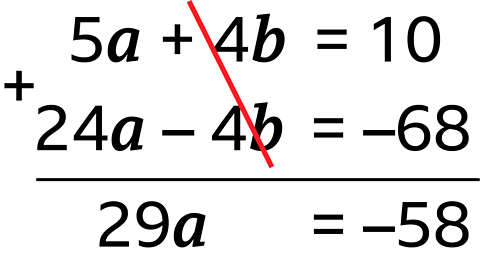
- Calculate the value of the remaining letter
\(29a = –58\)
\(a = –\frac{58}{29}\)
\(a = –2\)
- Substitute this back into one of the equations to find the value of the other letter
\(5a + 4b = 10\)
\(5(–2) + 4b = 10\)
\(–10 + 4b = 10\)
\(4b = 20\)
\(b = 5\)
This can be checked by substituting the values into the other equation.
\(6a – b = –17\)
\(6(–2) –5 = –17\) – this is correct
Question
Solve the simultaneous equations.
\(3a + 2b = 17\)
\(4a – b = 30\)
Answer
\(4a – b = 30 (\times 2) \rightarrow 8a – 2b = 60\)
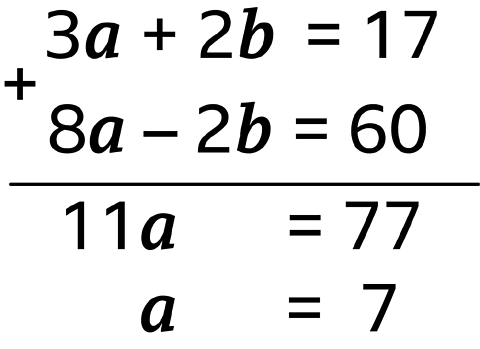
Same signs subtract, different signs add.
\(3a + 2b = 17\)
\(3(7) + 2b = 17\)
\(21 + 2b = 17\)
\(2b = 17 – 21\)
\(2b = –4\)
\(b = –2\)
Solution
\( a = 7\)
\( b = –2\)
- Check in the other equation to confirm
\(4(7) – (–2) = 30\) –this is correct
Creating and solving simultaneous equations
Simultaneous equations can be created to solve problems.
Example
Mr and Mrs Smith take their two children to the cinema. The total cost is ÂŁ33. Mr Jones takes his three children to the cinema and the total cost is ÂŁ27.50.
Calculate the price of a child's ticket and an adult's ticket.
Solution
Let \(a\) be the cost of an adult ticket and \(c\) the cost of a child’s ticket. There are two adults and two children in the Smith family, so the total cost can be described by the equation:
\(2a + 2c = 33\)
There is one adult and three children in the Jones family. The equation for the total cost is:
\(a + 3c = 27.5\)
Double the second equation to give a common coefficient of 2 for \(a\).
\(2a + 2c = 33\)
\(2a + 6c = 55\)
Decide whether to add or subtract the two equations by using the rule different add, same subtract (DASS).
\(2a + 6c = 55\)
\(2a + 2c = 33\)
To find the cost of an adult ticket, substitute the cost of a child ticket, ÂŁ5.50, into one of the original equations:
\(a + 3c = 27.5\)
\(a +3(5.5) = 27.5\)
\(a + 3 x 5.5 = 27.5\)
\(a + 16.50 = 27.50\)
\(a = 11\)
Check:
\(2a + 2c = 33\)
\(2(11) + 2(5.5) = 33\)
\(22 + 11 = 33\)
\(33 = 33\)
A child's ticket costs ÂŁ5.50 and an adult's ticket costs ÂŁ11.
Test yourself
More on M7: Algebra
Find out more by working through a topic
- count4 of 4