Equations and identities
An equation is a mathematical statement showing that two expressions are equal.
Equations can be solved by finding values (solutions) which make the statement true.
A linear equation has no terms raised to the power of 2 or higher. It has just one solution - one value that makes the equations true.
For example
\(y + 7 = 22\)
\(3m + 12 = 10 - m\)
\(3 (x - 1) = 27\)
A quadratic equation has at least one \(x^2\) term. In general, a quadratic equation has two solutions.
For example
\(x^2 = 9\)
\(3x^2 + x = 14\)
\(x^2 - 5x + 6 = 0\)
\(2 - 3x - 5x^2 = 0\)
An identity is a mathematical statement which is true for all values of a variable.
For example
\(5x + 4 = 3x + 2x + 3 + 1\) is an identity.
In this example, the right hand side (RHS) can be simplified to give the expression on the left hand side (LHS). Therefore, for any value of \(x\). the right hand side will always be the same as the left hand side.
The symbol \(\equiv\) is sometimes used to indicate an identity.
Other examples
\(3 (x - 2) = 3x - 6\)
\(x^2 - 9 = (x+3) (x-3)\)
\((x + 1) (x + 3) = x^2 + 4x + 3\)
Test yourself
Which of the following are identities?
A
\(3 (5x - 6) = 12\)
B
\(x^2 + 1 = 2 + x^2 -1\)
C
\(3 (2x + 4) = 2 (3x + 6)\)
D
\(x^2 - 2x - 2x - x^2\)
B and C are identities. Both sides of these give the same expression when simplified.
A is a linear equation and D is a quadratic equation.
Solving quadratic equations
The general form of a quadratic equation is
\(ax^2 + bx + c = 0\)
Where \(a\), \(b\) and \(c\) are numbers.
Both \(b\) and / or \(c\) can be equal to zero.
In this section, solving equations where \(a = 1\) will be considered.
To solve a quadratic equation
- rearrange the equation so that the RHS = 0
- factorise the LHS
- put the first factor equal to 0 and solve the linear equation
- put the second factor equal to 0 and solve the linear equation
- write down the two solutions
Example
Solve the equation \(x^2 - x = 5x\)
Solution
Rearrange the equation so that the RHS = 0
Subtract \(-5x\) from both sides to give 0 on RHS
Then simplify the LHS
\(x^2 - x - 5x = 5x - 5x\)
\(x^2 - 6x = 0\)
Factorise the LHS
\(x (x - 6) = 0\)
\(x\) is the common factor of \(x^2\) and \(6x\)
Put the first factor equal to 0 and solve the linear equation
\(x = 0\)
Put the second factor equal to 0 and solve the linear equation
\(x - 6 = 0\)
\(x = 6\)
Answer
Don't forget to give both solutions in your answer.
\(x = 6\) or \(0\)
Test yourself
Solve the equation \(x^2 + 3x + 7 = 7 - x\)
Rearrange the equation so the the RHS = 0
\(x^2 + 3x + 7 = 7 - x\)
Add \(-7 + x\) to both sides to get 0 on RHS
\(x^2 + 3x + 7 - 7 + x = 7 - x - 7 + x\)
\(x^2 = 4x = 0\)
Factorise the LHS
\(x (x + 4) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(x = 0\)
Put the second factor equal to 0 and solve the linear equation
\(x + 4 = 0\)
\(x = -4\)
Write down the two solutions
Answer
\(x = 0\) or \(x = -4\)
Example
Solve the equation \(x^2 + 12 = 7x\)
Solution
Rearrange the equation so that the RHS = 0
\(x^2 + 12 - 7x = 0\)
Change the order of the terms to the more familiar \( x^2 - bx + c = 0\) form.
It will be easier to factorise.
\(x^2 - 7x + 12 = 0\)
Factorise the LHS
\(x^2 - 7x + 12 = 0\)
Sum = \(-7\)
Product = \(+12\)
Key numbers are \(-4\) and \(-3\)
\((x - 4) (x - 3) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(x - 4 = 0\)
\(x = 4\)
Put the second factor equal to 0 and solve the linear equation
\(x - 3 = 0\)
\(x = 3\)
Answer
Write down the two solutions
\(x = 3\) or \(4\)
Test yourself
Solve the equation \(x^2 + 5x - 14 = 0\)
No need to rearrange the equation as the RHS is already equal to zero.
Factorise the LHS
\(x^2 + 5x - 14 = 0\)
Sum = \(+5\)
Product = \(-14\)
Key numbers are \(+7\) and \(-2\)
\((x + 7) (x - 2) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(x + 7 = 0\)
\(x = -7\)
Put the second factor equal to 0 and solve the linear equation
\(x - 2 = 0\)
\(x = 2\)
Write down the two solutions
Answer
\(x = -7\) or \(2\)
Example
Solve the equation \(x^2 - 16 = 0\)
Solution
No need to rearrange as RHS is already equal to zero.
Factorise the LHS - use the difference of two squares
\((x + 4) (x - 4) = 0\)
Put the first factor equal to 0 and solve the linear equation
\(x + 4 = 0\)
\(x = -4\)
Put the second factor equal to 0 and solve the linear equation
\(x - 4 = 0\)
\(x = +4\)
Answer
Write down the two solutions
\(x = -4\) or \(+4\)
Alternative solution
\(x^2 - 16 = 0\)
\(x^2 = 16\)
Take the square root of both sides
\(x = \sqrt{16}\)
Remember
\(\sqrt{x^2} = x\)
\(\sqrt{16} = + 4\) or \(-4\)
Don't forget the negative square root!
Answer
\(x = +4\) or \(-4\)
Test yourself
Solve the equation \(x^2 - 100 = 0\)
Solution
\(x^2 - 100 = 0\)
\(x^2 = 100\)
\(x = \sqrt{100} \)
\(x = +10\) or \(-10\)
Answer
\(x = +10\) or \(-10\)
or
Use DOTS
\(x^2 - 100 = 0\)
\((x + 10) (x - 10) = 0\)
\(x + 10 = 0\)
\(x = -10\)
\(x - 10 = 0\)
\(x = 10\)
Answer
\(x = +10\) or \(-10\)
Forming quadratic equations
For some questions an equation has to be formed and then solved.
Forming the equation is an important part of the question and no marks will be awarded for skipping the equations and guessing an answer, even if it is correct.
To form the equation, think about what you would do if the information had been given in numbers and do the same with the algebraic terms.
Example
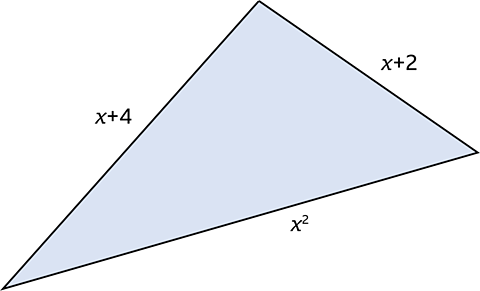
The diagram shows a triangle with sides measured in centimetres. The perimeter of the triangle is 21cm.
Form an equation and solve it to find the value of \(x\)
A solution by trial and improvement will not be accepted

Solution
The perimeter is the sum of the three sides.
\(P = x + 4 + x + 3 + x^2\)
Simplify \( = x^2 + 2x + 6\)
Perimeter = \(21 \)
\(x^2 + 2x + 6 = 21\)
Rearrange to have 0 on RHS
\(x^2 + 2 x - 15 = 0\)
Solve
Product = \(-15\)
Sum = \(+2\)
Key numbers are \(+5\) and \(-3\)
\(x^2 + 2x - 15 = (x + 5) (x - 3)\)
\(x + 5 = 0\)
\(x = -5\)
\(x - 3 = 0\)
\(x = 3\)
(\(x\) cannot equal \(-5\), this would make one of the sides negative in length as \(x + 4 = -1\))
Answer
\(x = 3cm\)

A quadratic equation usually has two solutions. In these types of questions, one of the answers will make sense and the other will not. Here, \(x = 3\) is the answer.
Test yourself
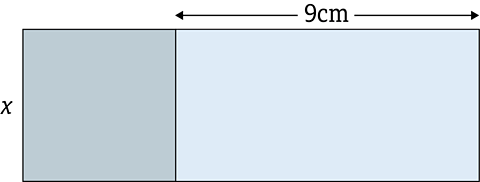
The diagram above shows a square with a side of \(x\) centimetres. Attached to the square is a rectangle whose longer side is 9 centimetres.
The area of the composite shape is 22cm².
Find the value of x.
A solution by trial and improvement will not be accepted.
Area of square = \(x^2\)
Area of rectangle = \(9x\)
Area of composite shape = \(x^2 + 9x\)
Area is given as \(22 cm^2\)
\(x^2 + 9x = 22\)
\(x^2 + 9x - 22 = 0\)
Product = \(-22\)
Sum = \(+9\)
Key numbers are \(+11\) and \(-2\)
\((x + 11) (x - 2) = 0\)
\(x + 11 = 0\)
\(x = -11\)
\(x - 2 = 0\)
\(x = 2\)
\(x = -11\) cannot be correct as a length cannot be negative
Answer
\(x = 2\)
The answer can be easily checked.
When \(x = 2\) the area of the square = \(4cm^2\)
Area of the rectangle is \(2 \times 9 = 18cm^2\)
Composite area = \(4 + 18 = 22cm^2\)
Test yourself
More on M3: Algebra
Find out more by working through a topic
- count5 of 5