An algebraic fraction is a fraction with algebraic terms in the numerator or the denominator or both.
Examples
\(\dfrac{3}{x}\)
\(\dfrac{x + 3}{x - 1}\)
\(\dfrac{12x}{5}\)
\(\dfrac{9x^2 - 1}{3x^2 - 2x - 1}\)
These topics are very useful
Adding and subtracting algebraic fractions
The same method is used for adding / subtracting both numerical fractions and algebraic fractions.
- Find a common denominator
- Write each fraction as an equivalent fraction with the common denominator
- Add the numerators of these equivalent fractions and keep the common denominator
Example
Simplify \(\dfrac{3a}{2} + \dfrac{7a}{3}\)
Solution
- Find a common denominator
The common denominator of 2 and 3 is 6
Write each fraction as an equivalent fraction with that common denominator.
Add the numerators of these equivalent fractions and keep the common denominator
\(\dfrac{9a}{6} + \dfrac{14a}{6} = \dfrac{23a}{6}\)
Answer
\(\dfrac{23a}{6}\)
Test yourself
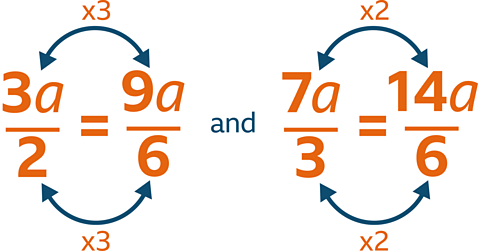
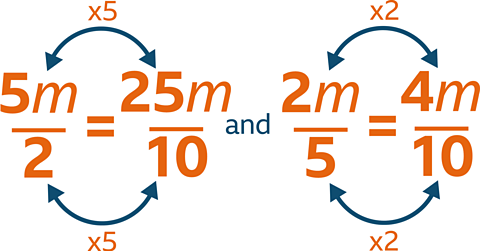
Simplify \(\dfrac{5m}{2} = \dfrac{2m}{5}\)
- Find a common denominator
Common denominator of 2 and 5 is 10
- Write each fraction as an equivalent fraction with that common denominator
\(\dfrac{5m}{2} + \dfrac{2m}{5} = \dfrac{25m}{10} + \dfrac{4m}{10}\)
- Add the numerators of these equivalent fractions and keep the common denominator
\( \dfrac{25m}{10} + \dfrac{4m}{10} = \dfrac{29m}{10}\)
Answer
\(\dfrac{29m}{10}\)
Example
Simplify \(\dfrac{x + 1}{4} + \dfrac{2 (x + 5)}{3}\)
Solution
This sample looks harder because of the more complex terms in the numerator, but the method is just the same. An extra final step will be needed to simplify the numerator.
- Find a common denominator
Common denominator of 4 and 3 is 12
- Write each fraction as an equivalent fraction with that common denominator
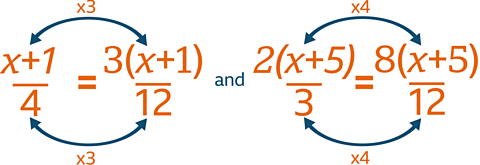
- Add the numerators of these equivalent fractions and keep the common denominator
\(\dfrac{3 (x + 1)}{12} + \dfrac{8 (x + 5)}{12} = \dfrac{3 (x + 1 ) + 8(x + 5)}{12}\)
- Simplify the numerator
\( = \dfrac{3x + 3 + 8x + 40}{12}\)
\( = \dfrac{11x + 43}{12}\)
Answer
\( \dfrac{11x + 43}{12}\)
Test yourself
Simplify \( \dfrac{2 (2x - 5)}{5} - \dfrac{3 (x - 1)}{2}\)
- Find a common denominator
Common denominator of 5 and 2 is 10
- Write each fraction as an equivalent fraction with that common denominator
\(\dfrac{2 (2x - 5}{5} - \dfrac{n3 (x - 1)}{2} = \dfrac{4 (2x - 5}{10} - \dfrac{15 (x - 1)}{10}\)
\(\dfrac{2}{5} = \dfrac{4}{10}\) and \(\dfrac{3}{2} = \dfrac{15}{10}\)
- Add the numerators of these equivalent fractions and keep the common denominator
\( \dfrac{4 (2x - 5}{10} - \dfrac{15 (x - 1)}{10} = \dfrac{4 (2x - 5) - 15 (x - 1)}{10}\)
- Simplify the numerator
\(\dfrac{8x - 20 - 15x +15}{10}\)
\(\dfrac{-7x - 5}{10}\)
Answer
\(\dfrac{-7x - 5}{10}\)
Simplifying, multiplying and dividing algebraic fractions
The method used for multiplying or dividing algebraic fractions is similar to the method for numerical fractions.
However some expressions may need to be factorised at the start and the solution may need to be simplified before presenting the answer.
- Factorise any expression which requires it
- Look for any common factors shared by numerator and denominator
- Divide top and bottom by any common factor
- Simplify where necessary
Example
Simplify \(\dfrac{3x}{9x + 6x^2}\)
Solution
Factorise where possible
\(9x + 6x^2\)
can be factorised to give
\(3x (3 + 2x)\)
\(\dfrac{3x}{9x + 6x^2} = \dfrac{3x}{3x (3 + 2x)}\)
Look for a common factor that the numerator and denominator shares.
\(3x\) is a common factor
Divide top and bottom by that common factor
\(\dfrac{3x}{3x (3 + 2x)} = \dfrac{1}{(3 = 2x)}\)
Simplify where necessary
\(\dfrac{1}{(3 = 2x)}\) cannot be simplified
Answer
\(\dfrac{1}{(3 = 2x)}\)
The brackets are no longer essential.
An answer of \(\dfrac{1}{3 = 2x}\)
is equally correct.
Test yourself
Simplify \(\dfrac{x^2 + 2x}{x^2 - 3x}\)
Factorise any expression requiring it
Both numerator and denominator can be factorised
\(\dfrac{x^2 + 2x}{x^2 - 3x} = \dfrac{x (x + 2)}{x (x - 3)}\)
Look for a common factor shared by numerator and denominator
\(x\) is a common factor
Divide top and bottom by that common factor
\( \dfrac{x (x + 2)}{x (x - 3)} = \dfrac{(x - 2)}{(x - 3)}\)
Simplify where necessary
\(\dfrac{(x - 2)}{(x - 3)}\) cannot be simplified
Answer
\(\dfrac{(x - 2)}{(x - 3)}\)
Example
Simplify \(\dfrac{(x^2 - 24)}{(2x + 10)}\)
Solution
Factorise any expression which requires it
\(x^2 - 25\) can be factorised to give \((x + 5) (x - 5)\)
\(2x + 10\) can be factorised to give \(2 (x + 5)\)
\(\dfrac{(x^2 - 25)}{(2x + 10)} = \dfrac{(x + 5) (x - 5)}{2 (x + 5)}\)
Look for a common factor shared by numerator and denominator
\((x + 5)\) is a common factor
Divide top and bottom by that common factor
\(\dfrac{(x + 5)(x - 5)}{2 (x - 5)} = \dfrac{(x - 5)}{2}\)
Simplify where necessary
\(\dfrac{(x - 5)}{2}\) cannot be simplified
Answer
\(\dfrac{(x - 5)}{2}\)
Remember
Difference of two squares
\(a^2 - b^2 = (a + b)(a - b)\)
(this reminder should maybe be in the solution block)
Test yourself
Simplify \(\dfrac{(x^2 + 6x + 5)}{(x^2 - x - 2)}\)
Factorise any expression requiring it
Both expressions can be factorised
\(x^2 + 6x + 5 = (x + 5)(x + 1)\)
To factorise
Product = \(5\)
Sum = \(6\)
Find two numbers that add to give 5 and multiply to give 6
\(5 \times 1 = 5\)
\(5 + 1 = 6\)
\(x^2 - x - 2 = (x + 1) (x - 2)\)
To factorise
Product = \(-2\)
Sum = \(-1\)
Find two numbers that add to give \(-1\) and multiply to give \(-2\)
\(-2 \times 1 = -2\)
\(-2 + 1 = -1\)
\(\dfrac{(x^2 + 6x + 5)}{x^2 - x - 2)} = \dfrac{(x + 5)(x + 1)}{(x + 1)(x - 2)}\)
Look for a common factor shared by numerator and denominator
\((x + 1)\) is a common factor
Divide top and bottom by that common factor
\(\dfrac{(x + 5)(x + 1)}{(x + 1)(x - 2)} = \dfrac{[x + 5)}{[x - 2)}\)
Simplify where necessary
\(\dfrac{(x + 5)}{(x - 2)}\) cannot be simplified
Answer \(\dfrac{(x + 5)}{(x - 2)}\)
Test yourself
More on M3: Algebra
Find out more by working through a topic
- count5 of 5